Written by Adam Burke

---

It’s not often that I go to an Indians game and go the duration of the game without hearing somebody say something stupid or completely wrong about baseball. Wednesday was not the exception. The Indians trailed 2-1 in the second inning against Justin Verlander and the Tigers. Mark Reynolds singled to left and Ryan Raburn drove Torii Hunter to the wall in right field to single on a ball that Hunter should have caught. The Indians had two on and nobody out with Yan Gomes coming to the plate.

Let’s evaluate the entire scenario. Ubaldo Jimenez was on the mound for the Indians and he didn’t look sharp. The Tigers were going to score more runs. Yan Gomes unsuccessfully tried to bunt last Monday in the 10th inning before hitting a walk-off three-run homer. Gomes entered this at bat hitting .302 with a .642 slugging percentage. Verlander, for once, was not sharp and had just given up a 385-foot fly ball to a guy who has had below average power throughout his career, averaging one home run every 28.2 at bats. Oh, yeah, and IT’S THE SECOND INNING.

Gomes fouled off the first pitch. “WHY ISN’T HE BUNTING?!” a voice roared to my left. Rather than confuse this guy with the long list of reasons why Gomes shouldn’t be asked to bunt in this situation, I watched eagerly, hoping Gomes would crush a three-run shot to prove this guy wrong. Gomes worked the count to 3-1 before hitting a laser beam to left center that Andy Dirks ran down for the first out. Michael Bourn would follow with a single that plated Reynolds easily and sent Ryan Raburn to third with one out. Jason Kipnis struck out, Asdrubal Cabrera walked, and Michael Brantley grounded out to end the inning.

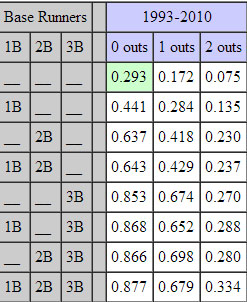
Compiled by Tom Tango, the run expectancy matrix presents both the average number of runs from that point to the end of the inning and the percentage chance (in decimal values) of a run being scored given the number and placement of baserunners.

On the left is the average number of runs scored in a given scenario through the end of the inning. On the right is the percentage chance of a run scoring at some point in the inning.

     

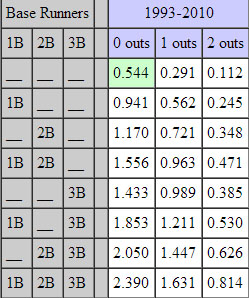
Let’s revisit the Yan Gomes situation. There were runners on first and second with nobody out. The run expectancy matrix puts the average number of runs in that scenario at 1.556 in that inning. Let’s say that Gomes successfully advanced both runners with a sacrifice bunt. The expected average number of runs scored in that inning would drop to 1.447. Not a substantial drop, but significant enough to consider a bunt to be a negative and rather short-sighted.

If you’ve looked at both images, the logical thing to do would be to look at the chart on the right and say, “But, wait. This chart says we have a better chance of scoring a run with a sacrifice bunt.” You’re right. If Gomes successfully sacrificed, the chances of scoring a run would go from 64.3 percent to 69.8 percent. A five percent increase is significant.

This is where the “IT’S THE SECOND INNING” part comes into play. The run expectancy matrix is spitting out the percentage chance of scoring “a” run. Not multiple runs. A run. One. One run. You would be playing for one run. By letting Gomes swing away, you increase your chances of scoring multiple runs. Sure, you may not score in that inning no matter what happens. But, you’ve still got seven innings and 21 outs to play with.

It’s easy for me to cherry pick this example because Gomes got ahead in the count, 3-1, and ripped a rocket to left field that very easily could have gone for a RBI double that would have left runners on second and third with nobody out. But, that’s the caveat. If you force the batter to bunt, you have no idea what may have happened by swinging away. You’re just giving up an out. In the Moneyball generation of baseball, hitting is all about not making outs. That’s why there’s so much emphasis on drawing walks.

Invariably, somebody out there reading this is saying, “He could have hit into a double play.” And, they’re absolutely right. This is why game theory comes into play. Sometimes called game state, it’s nothing more than weighing the risk-reward. It just so happened that Gomes has been hitting well of late. If it had been somebody like Brendan Ryan or Ezequiel Carrera at the plate, then a bunt is probably a higher percentage play than with somebody like Gomes, who has very little experience in bunting. Gomes may have hit into a double play. He also may have bunted the ball foul twice and subsequently struck out, dropping the run expectancy from 1.556 to 0.963 and the chance of scoring a run from 64.3 percent to 42.9 percent.

The Tigers’ four-run outburst in the third supported Francona’s decision not to call for the bunt, as one run wouldn’t have meant much after that. The argument could be made that a successful sacrifice bunt allows two runners to score on Bourn’s single. That, of course, is hindsight being 20/20. We could also discuss how Raburn ending up on third with less than two outs, and then Bourn stealing second, had essentially the same effect as the bunt without giving up an out. With nobody out in the third inning, the right play is to play for the big inning, not give up outs. Had that situation come up in the eighth or ninth inning, everything changes. Gomes may have been lifted for a pinch hitter who was a better bunter.

Context makes a big difference. The Indians have one of the most explosive offenses in baseball so far, averaging just shy of 5.3 runs per game. They have the potential to put up big innings. Other teams, like the Pirates, may be better off playing for every run that they can get because they don’t have home run hitters or many extra base hit threats.

There are a lot of situations where fans instantly call for a bunt. One of the biggest is with a runner on second and nobody out. Referring back to the charts, the average number of runs in an inning drops from 1.17 to 0.989 with a sacrifice bunt that advances the runner to third. The percentage chance of that runner who was on second with nobody out scoring is 63.7 percent. A sacrifice bunt improves that chance to 67.4 percent. A walk to put runners at first and second bumps the run expectancy to 1.556 and a single with the runner stopping at third bumps the run expectancy to 1.853. A RBI single would be a run plus an average of 0.941 runs more in the inning.

One of my biggest pet peeves in baseball is when there’s a runner on second and a left handed batter is called on to bunt him over.  For one thing, a ball pulled on the ground to the right side or hit deep enough to right field is going to advance the runner anyway without giving up an out. For another thing, said ground ball could be pulled through the hole for a RBI single, or, at worst, runners on the corners without wasting an out. Hell, every right handed hitter should be able to inside-out a ball to the right side to advance the runner or even get a base hit.

Outs are precious. The goal should be to give up as few of them as possible over the course of a season. It’s a risk-reward thing. Over the last few seasons, the Indians may have been better off playing for one or two runs instead of the big inning. But this season, in a lineup where everybody has an on-base percentage above .300, giving up outs is generally a bad idea.

To take this bunting argument one step further, I’ll introduce another advanced statistic called “Win Probability Added” or WPA. Everything that happens in a baseball game either increases a team’s chance of winning or decreases a team’s chance of winning. One of the flaws of WPA is that it assumes everything is equal, so, for example, if the Indians have Justin Masterson on the mound and the Tigers have Rick Porcello, there’s no way of indicating that Masterson is better than Porcello. Similarly, using Wednesday night as an example, there’s no way of telling WPA that the pitching matchup is Justin Verlander against Ubaldo Jimenez.

Back to the Gomes example. To refresh your memory, the Indians, the home team, are down 2-1, with runners on first and second and nobody out. The Hardball Times has a WPA Calculator. You can enter two scenarios and see the difference in win probability based on what occurred. (Realistically, the "Runs/Game" should be higher between the Tigers and Indians. I'll spare you the explanation since there are a lot of numbers and concepts in here already, but it will affect the WPA because the score differential can mean more or mean less depending on the pitching matchup or the teams. The value I chose of 3.5 is a little bit lower, but this is just to illustrate my overall point about bunting.)

As you can see, the top line is before Gomes’s at bat. Even trailing 2-1, the Indians have a 53.04 percent chance of winning the game. Had Gomes bunted, even with advancing the runners, the win probability would have dropped to 52.86 percent.

Let’s compare a successful sacrifice bunt to what Gomes did, which was fly out without advancing either runner.

A successful bunt was clearly more valuable than the fly out, but the Indians still have a 46.45 percent chance of winning the game, because it’s the second inning. Their win probability dropped by six percent, which would be substantial late in the game, but in the second inning, it’s far less significant.

As I’ve already discussed, Gomes got ahead in the count and hammered a ball that just happened to be caught. What if that ball would have fallen in for a game-tying single?

I’ll say that Raburn would have stopped at second, so the Indians have increased their chances of winning by nearly 12 percent. Had Raburn gone to third, the Indians’ win probability would have jumped all the way to 69 percent, nearly a 17 percent increase.

This is a rather simplified look at bunting and its effect on a game, but it’s clear to see that there are times where bunting can be a helpful decisions and times where it can hurt a team’s chances to win the game. That’s assuming that all bunt decisions work out. Average bunters are successful at advancing runners around 75 percent of the time. How often do we see a bunt popped up or bunted too hard and the lead runner gets forced out? If bunts were foolproof, they’d be a more favorable option, but bunts are far from foolproof, especially for hitters like Yan Gomes.

Overall, I’m anti-bunt and it’s backed up by statistical analysis. I realize there are spots where game theory and game state dictate a bunt and that it’s the best possible option. But those spots are few and far between. Even a ninth inning sacrifice bunt with runners on first and second in a tie game only improves a team’s win probability by four percent. It’s not that it’s a bad thing to improve your chances of winning, but it’s drastically overestimated.

I hope the guy who yelled in favor of a second inning bunt has read this.